Gráficos em ciência da computação: definição, tipos, exemplos de aplicações. teoria dos grafos em ciência da computação

Contagens no método de computador para as relações que determinam são elementos combinados. Estes são os objetos básicos de estudo na teoria dos grafos.

definições básicas

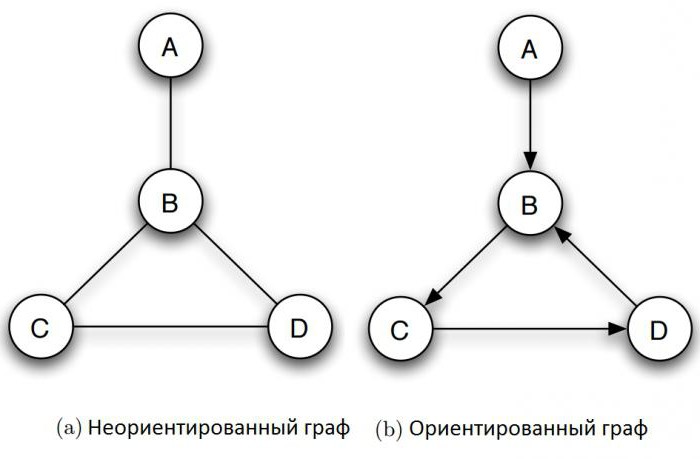
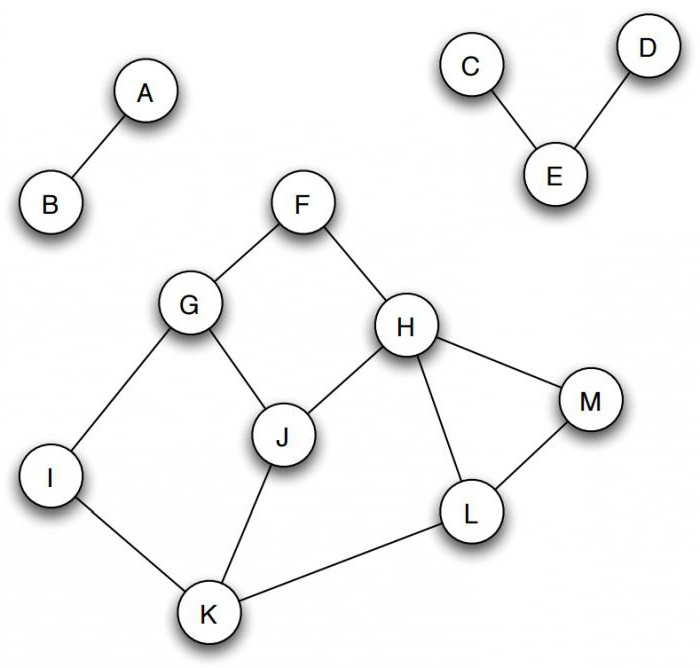
Qual é o gráfico em ciência da computação? Ele inclui uma pluralidade de objectos chamados nodos ou vértices, alguns pares de que são ligadas por m. N. costelas. Por exemplo, o gráfico na figura (a) consiste de quatro nodos, denotadas A, B, C, e D, B dos quais está ligado a cada um dos outros três vértices costelas, e C e D também são ligados. Dois nós são adjacentes se eles estão ligados por uma aresta. A figura mostra uma maneira típica de como construir gráficos em ciência da computação. Os círculos representam os vértices e as linhas ligando cada par deles, são as costelas.

O grafo não direcionado é chamado em ciência da computação? Ele relações entre as duas extremidades das costelas são simétricas. Rib simplesmente conecta-los uns com os outros. Em muitos casos, no entanto, que é necessário para exprimir a relação assimétrica – por exemplo, que uma pontos a B, mas não vice-versa. Este objectivo é a definição do gráfico no computador, ainda é constituído de um conjunto de nodos com um conjunto de arestas dirigidas. Cada aresta orientada é a ligação entre os vértices cuja direcção tem significado. grafos dirigidos descrevem, como mostrado na Figura (b), as suas bordas são representadas por setas. Quando você quiser enfatizar que grafo não-direcional, é chamado de não-direcionado.

modelos de rede

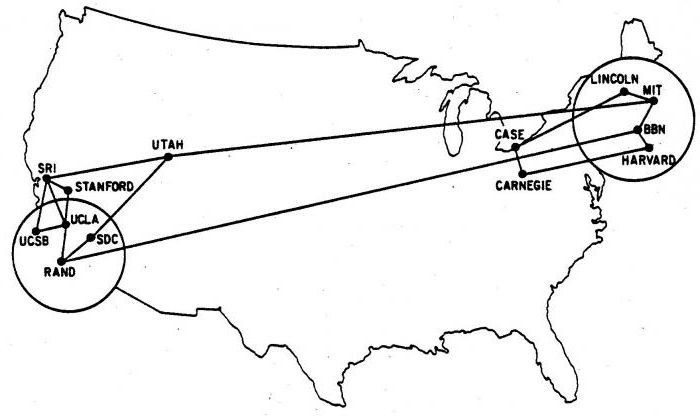
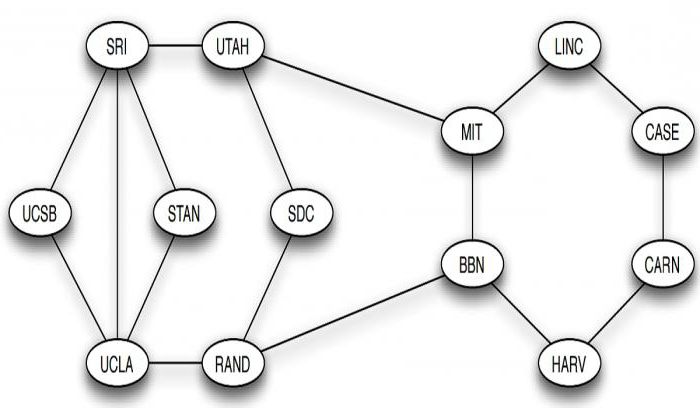
Gráficos em ciência da computação são modelo matemático de estruturas de rede. A figura a seguir mostra a estrutura da Internet, em seguida, tinha o nome da ARPANET, em dezembro de 1970, quando ela tinha apenas 13 pontos. Os nós estão processando centros e as costelas se conectar a dois vértices feedforward entre as mesmas. Se você não prestar atenção para os Estados Unidos impuseram o mapa, o resto da imagem é um gráfico de 13 nó semelhante ao anterior. Neste caso, a posição real do vértice não é essencial. É importante que os nós são conectados uns aos outros.

Aplicação de gráficos no computador permite ver como as coisas são ou interligados fisicamente ou logicamente em uma estrutura de rede. 13-nó ARPANET é um exemplo de rede de comunicação em que os computadores de topo ou outros dispositivos podem transmitir mensagens, e as bordas representam link direto em que a informação pode ser transmitida.

rotas

Embora os gráficos são usados em muitas áreas diferentes, eles têm características comuns. teoria dos grafos (informática) inclui talvez o mais importante deles – a idéia de que muitas vezes as coisas se movem ao longo das bordas, sequencialmente passando de nó em nó, seja ele um passageiro alguns voos ou informações transmitidas de pessoa para pessoa em uma rede social, ou um usuário computador, de forma consistente visitar um número de páginas da web, seguindo os links.

Esta ideia motiva a definição da rota como uma série de nós conectados por arestas. Às vezes, é necessário considerar a rota que não contém apenas componentes, mas também a seqüência de arestas conectando-os. Por exemplo, a sequência de vértices MIT, BBN, RAND, UCLA é um percurso em gráfico internet ARPANET. Passagem de nós e arestas pode ser repetido. Por exemplo, SRI, STAN, UCLA, SRI, Utah, MIT também é uma rota. A maneira em que as costelas não se repitam, chamado de uma cadeia. Se os nós não se repitam, é chamado de uma cadeia simples.

ciclos

espécies particularmente importantes em gráficos de computador – ciclos que representam uma estrutura de anel, tais como uma sequência de nós LINC, PROCESSO, CARN, HARV, BBN, MIT, LINC. Rotas com pelo menos três costelas, em que o primeiro e último nó são os mesmos, e os restantes são diferentes, representam um gráficos cíclicos em ciência da computação.

Exemplos: ciclo SRI, STAN, UCLA, SRI é o mais curto, e SRI, STAN, UCLA, RAND, BBN, Utah, SRI consideravelmente maior.

Praticamente todos os borda ARPANET do gráfico pertence ao ciclo. Isso foi feito deliberadamente, se algum deles falhar, terá a possibilidade de transição de um nó para outro. Ciclos nas comunicações e sistemas de transporte estão presentes para redundância – eles fornecem rotas alternativas para um outro caminho ciclo. As redes sociais são frequentemente ciclos perceptíveis. Quando você encontrar, por exemplo, que um amigo da escola perto de um primo de sua esposa realmente funciona com o seu irmão, é um ciclo que consiste em você, sua esposa, seu primo, seu amigo de escola, seu empregado (ie. E. Seu irmão), e finalmente você novamente.

grafo conexo: definição (informática)

É natural querer saber se é possível a partir de cada nó para chegar a qualquer outro nó. O gráfico está ligado se existe um caminho entre cada par de vértices. Por exemplo, a rede ARPANET – ligado gráfico. O mesmo pode ser dito sobre a maioria das redes de comunicação e de transporte, como sua finalidade é direcionar o tráfego a partir de um nó para outro.

Por outro lado, não há uma razão a priori para esperar que esses tipos de gráficos em ciência da computação são generalizadas. Por exemplo, na rede social não é difícil imaginar duas pessoas que não estão relacionados entre si.

componentes

Se a coluna não está ligado ao computador, eles naturalmente cair em um conjunto de fragmentos relacionados, grupos de nós que são isoladas e não se cruzam. Por exemplo, a Figura mostra três de tais partes: a primeira – A e B, a segunda – C, D e E, e a terceira consiste nos vértices restantes.

Componentes do gráfico representam um subconjunto de nós, em que:

• cada subgrupo vértice tem um percurso de qualquer outro;
• subconjunto não é parte de um conjunto maior, em que cada nó tem uma rota para qualquer outro.

Quando os gráficos em computador são divididos em seus componentes, é apenas a descrição inicial do método de sua estrutura. Este componente pode ser rico na estrutura interna, é importante para a interpretação da rede. Por exemplo, o método formal de determinar a importância nó é determinar quantas partes serão divididos contagem, se o nó é removido.

componente máxima

Há um método para avaliação qualitativa dos componentes de conectividade. Por exemplo, não é uma rede social do mundo, com conexões entre duas pessoas, se eles são amigos.

É conectado? Provavelmente não. Conectividade – propriedade bastante frágil, e o comportamento de um nó (ou um pequeno conjunto deles) pode reduzi-la a nada. Por exemplo, uma única pessoa sem amigos que vivem é um componente constituído por um único vértice, e, portanto, a contagem não será conectado. Ou uma remota ilha tropical, composto por pessoas que não têm contato com o mundo exterior, também será um pequeno componente da rede, o que confirma a sua incoerência.

rede global de amigos

Mas há algo mais. Por exemplo, um leitor do livro popular tem amigos que cresceram em outros países, e os torna um componente. Se levarmos em conta os pais desses amigos e seus amigos, todas essas pessoas também estão no mesmo componente, embora nunca tinha ouvido falar sobre o leitor, falam uma língua diferente, e ao lado dele nunca foi. Assim, embora a rede global de amizade – não está ligado, o leitor será incluído no componente são muito grandes, penetrando todas as partes do mundo, que inclui pessoas de muitas origens diferentes e, na verdade, contém uma parcela significativa da população mundial.

O mesmo ocorre nos conjuntos de dados de rede – grandes redes complexas, muitas vezes têm um componente máxima, que inclui uma proporção significativa de todos os nós. Além disso, quando a rede inclui um componente máxima, é quase sempre um só. Para entender o porquê, é necessário voltar ao exemplo de uma rede global de amizade e tentar imaginar a existência de dois componentes máximo, cada um dos quais envolve milhões de pessoas. Ele precisa ter uma única costela em algum do primeiro componente para o segundo a um máximo de dois componentes fundidos em um. Uma vez que apenas uma extremidade, na maioria dos casos é improvável que não foi formada, e, portanto, no máximo, dois componentes em redes reais nunca são observados.

Em alguns casos raros, quando os dois componentes da máxima de co-existido por um longo tempo em uma rede real, a sua união foi inesperado, dramático, e, finalmente, ter consequências catastróficas.

fusão componente acidente

Por exemplo, após a chegada de exploradores europeus na civilização do Hemisfério Ocidental cerca de metade de um milênio atrás, houve um cataclismo global. Do ponto de vista da rede, ele ficou assim: cinco mil anos de rede social global, provavelmente consistia de dois componentes gigante – um no Norte e América do Sul, e os outros – na Eurásia. Por esta razão, a tecnologia tem evoluído de forma independente nos dois componentes, e, pior ainda, como desenvolvido e doença humana, e assim por diante. D. Quando os dois componentes finalmente em tecnologia de toque e uma doença de forma rápida e desastrosamente transbordou segundo.

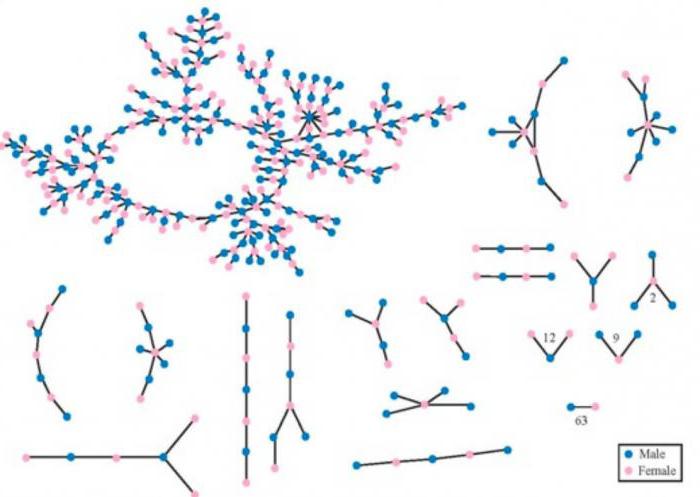
High School americana

O conceito da máxima componente é útil para o raciocínio sobre redes em uma escala muito menor. Um exemplo interessante é um gráfico que ilustra a relação em uma escola secundária dos Estados Unidos para o período de 18 meses. O fato de que ele contém o componente máxima é essencial quando se trata da propagação de doenças, doenças sexualmente transmissíveis, que é o objetivo do estudo. Os estudantes podem ter tido apenas um parceiro durante esse período de tempo, mas, no entanto, sem perceber, ter sido parte dos componentes do máximo e, portanto, uma parte de muitas rotas potenciais de transmissão. Estas estruturas refletem uma relação que pode ter longa terminou, mas eles se conectam indivíduos em cadeias muito tempo, para ser objecto de intenso escrutínio e fofocas. No entanto, eles são reais: como os fatos sociais são invisíveis, mas macroestruturas consequentes surgiu como um produto de mediação individual.

Distância e em largura pesquisa

Além da informação sobre se dois nós são conectados rota, teoria dos grafos em ciência da computação permite que você aprenda sobre seu comprimento – no transporte, comunicação ou divulgação de notícias e doenças, bem como se ele passa por vários picos ou múltipla.

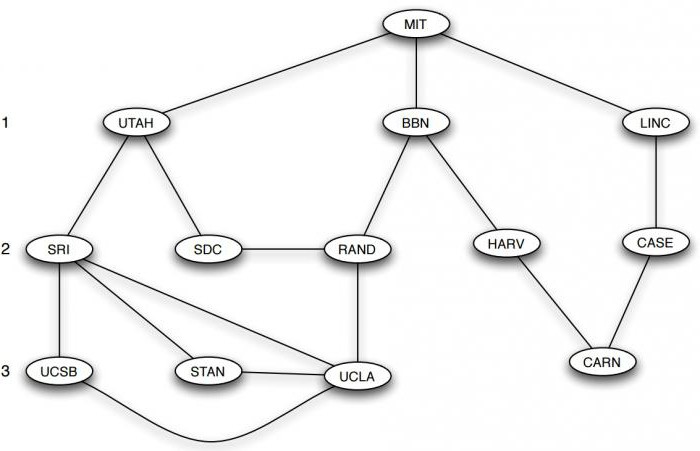
Para fazer isso, definir um comprimento de percurso igual ao número de passos que contém do início ao fim, ou seja,. E. O número de arestas na sequência que é. Por exemplo, MIT, BBN, RAND, rota UCLA tem um comprimento de 3, e MIT, UTAH – 1. Usando o comprimento do caminho, podemos dizer que se dois nós estarem dispostos na coluna perto uns dos outros ou muito distância entre os dois picos é definido como o comprimento de o caminho mais curto entre eles. Por exemplo, a distância entre o LINC e SRI é 3, no entanto, para garantir que esta, é necessário verificar a ausência de comprimento igual a 1 ou 2, entre os mesmos.

Em largura algoritmo de busca

Para pequena distância gráfico entre dois nós calcular facilmente. Mas para complexo há uma necessidade de um método sistemático de determinar distâncias.

A maneira mais natural para fazer isso e, portanto, o mais eficaz é o seguinte (por exemplo, uma rede global de amigos):

• Todos os amigos são declarados localizado a uma distância de 1.
• Todos os amigos de amigos (sem contar o já mencionado) são anunciados à distância 2.
• Todos os seus amigos (novamente, sem contar as pessoas rotuladas) anunciou na distância remota 3.

Continuando desta maneira, a busca é realizada em camadas subsequentes, cada um dos quais – na unidade em que o anterior. Cada nova camada é composta por nós que não participaram nas anteriores, e que cair borda do vértice da camada anterior.

Esta técnica é chamada de busca em largura primeiro, como ela procura para a coluna fora do nó inicial, cobrindo principalmente a próxima. Além de fornecer um método para determinar distâncias, que pode servir como um quadro conceitual útil para organizar a estrutura de gráfico, bem como a forma de construir um gráfico do computador, tendo picos com base na sua distância a partir de um ponto de partida fixo.

procura em largura pode ser aplicado não só a uma rede de amigos, mas também para qualquer gráfico.

mundo pequeno

Se você voltar a uma rede global de amigos, você pode ver que o argumento de que explica que pertence ao componente máxima realmente aprova algo mais: não só o leitor tem rotas para amigos, ligando-o com uma proporção significativa da população mundial, mas estas rotas são surpreendentemente curto .

Esta ideia é chamado de "pequeno fenômeno mundial": o mundo parece pequeno, se você pensar sobre o que uma rota curta conecta duas pessoas.

A teoria de "seis apertos de mão" foi primeiro experimentalmente investigado por Stanley Milgram e seus colegas na década de 1960. Sem ter qualquer conjunto de dados de redes sociais, e com um orçamento de US $ 680, ele decidiu verificar uma ideia popular. Para este fim, ele pediu 296 iniciadores selecionados aleatoriamente tentar enviar uma carta para o corretor, que vivia em um subúrbio de Boston. Iniciadores foram dadas algumas informações pessoais sobre o efeito (incluindo endereço e profissão), e eles tiveram que enviar uma carta para a pessoa que eles conheciam pelo nome, com as mesmas instruções, para que ele atingiu a meta o mais rápido possível. Cada letra passou pelas mãos de um número de amigos e formaram uma corrente fecha para corretores da bolsa fora de Boston.

Entre as 64 cadeias que atingiram o alvo, a duração média foi de seis, confirmando o número de nomeados duas décadas anteriores na peça título Dzhona Gera.

Apesar de todas as limitações deste estudo, o experimento demonstrou um dos aspectos mais importantes da nossa compreensão das redes sociais. Nos anos que se seguiram a partir dele foi feito conclusão mais ampla: redes sociais tendem a ter rotas muito curtos entre pares arbitrários de pessoas. E mesmo se tais conexões indiretas com líderes empresariais e líderes políticos não se pagam em uma base diária, a existência de tais rotas curtas desempenha um grande papel na velocidade de disseminação de informações, doenças e outros tipos de infecção na comunidade, bem como o acesso as oportunidades que a rede social oferece às pessoas bastante as qualidades opostas.